norse.torch.module package

Modules for spiking neural network, adhering to the torch.nn.Module interface.

class norse.torch.module.CobaLIFCell(input_size, hidden_size, p=CobaLIFParameters(tau_syn_exc_inv=tensor(0.2000), tau_syn_inh_inv=tensor(0.2000), c_m_inv=tensor(5.), g_l=tensor(0.2500), e_rev_I=tensor(- 100), e_rev_E=tensor(60), v_rest=tensor(- 20), v_reset=tensor(- 70), v_thresh=tensor(- 10), method='super', alpha=100.0), dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Module that computes a single euler-integration step of a conductance based LIF neuron-model. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/c_{\text{mem}} (g_l (v_{\text{leak}} - v) + g_e (E_{\text{rev_e}} - v) + g_i (E_{\text{rev_i}} - v)) \\ \dot{g_e} &= -1/\tau_{\text{syn}} g_e \\ \dot{g_i} &= -1/\tau_{\text{syn}} g_i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ g_e &= g_e + \text{relu}(w_{\text{input}}) z_{\text{in}} \\ g_e &= g_e + \text{relu}(w_{\text{rec}}) z_{\text{rec}} \\ g_i &= g_i + \text{relu}(-w_{\text{input}}) z_{\text{in}} \\ g_i &= g_i + \text{relu}(-w_{\text{rec}}) z_{\text{rec}} \\ \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input.

  • hidden_size (int) – Size of the hidden state.

  • p (LIFParameters) – Parameters of the LIF neuron model.

  • dt (float) – Time step to use.

Examples

>>> batch_size = 16
>>> lif = CobaLIFCell(10, 20)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = lif(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, state=None)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

Return type

Tuple[Tensor, CobaLIFState]

training: bool
class norse.torch.module.CobaLIFParameters(tau_syn_exc_inv: torch.Tensor = tensor(0.2000), tau_syn_inh_inv: torch.Tensor = tensor(0.2000), c_m_inv: torch.Tensor = tensor(5.), g_l: torch.Tensor = tensor(0.2500), e_rev_I: torch.Tensor = tensor(- 100), e_rev_E: torch.Tensor = tensor(60), v_rest: torch.Tensor = tensor(- 20), v_reset: torch.Tensor = tensor(- 70), v_thresh: torch.Tensor = tensor(- 10), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parameters of conductance based LIF neuron.

Parameters

  • tau_syn_exc_inv (torch.Tensor) – inverse excitatory synaptic input time constant

  • tau_syn_inh_inv (torch.Tensor) – inverse inhibitory synaptic input time constant

  • c_m_inv (torch.Tensor) – inverse membrane capacitance

  • g_l (torch.Tensor) – leak conductance

  • e_rev_I (torch.Tensor) – inhibitory reversal potential

  • e_rev_E (torch.Tensor) – excitatory reversal potential

  • v_rest (torch.Tensor) – rest membrane potential

  • v_reset (torch.Tensor) – reset membrane potential

  • v_thresh (torch.Tensor) – threshold membrane potential

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of CobaLIFParameters(tau_syn_exc_inv, tau_syn_inh_inv, c_m_inv, g_l, e_rev_I, e_rev_E, v_rest, v_reset, v_thresh, method, alpha)

alpha: float

Alias for field number 10

c_m_inv: torch.Tensor

Alias for field number 2

e_rev_E: torch.Tensor

Alias for field number 5

e_rev_I: torch.Tensor

Alias for field number 4

g_l: torch.Tensor

Alias for field number 3

method: str

Alias for field number 9

tau_syn_exc_inv: torch.Tensor

Alias for field number 0

tau_syn_inh_inv: torch.Tensor

Alias for field number 1

v_reset: torch.Tensor

Alias for field number 7

v_rest: torch.Tensor

Alias for field number 6

v_thresh: torch.Tensor

Alias for field number 8

class norse.torch.module.CobaLIFState(z: torch.Tensor, v: torch.Tensor, g_e: torch.Tensor, g_i: torch.Tensor)[source]

Bases: tuple

State of a conductance based LIF neuron.

Parameters

Create new instance of CobaLIFState(z, v, g_e, g_i)

g_e: torch.Tensor

Alias for field number 2

g_i: torch.Tensor

Alias for field number 3

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.module.ConstantCurrentLIFEncoder(seq_length, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Encodes input currents as fixed (constant) voltage currents, and simulates the spikes that occur during a number of timesteps/iterations (seq_length).

Example

>>> data = torch.as_tensor([2, 4, 8, 16])
>>> seq_length = 2 # Simulate two iterations
>>> constant_current_lif_encode(data, seq_length)
(tensor([[0.2000, 0.4000, 0.8000, 0.0000],   # State in terms of membrane voltage
        [0.3800, 0.7600, 0.0000, 0.0000]]),
tensor([[0., 0., 0., 1.],                   # Spikes for each iteration
        [0., 0., 1., 1.]]))
Parameters

  • seq_length (int) – The number of iterations to simulate

  • p (LIFParameters) – Initial neuron parameters.

  • dt (float) – Time delta between simulation steps

forward(input_currents)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.Izhikevich(spiking_method, **kwargs)[source]

Bases: norse.torch.module.snn.SNN

A neuron layer that wraps a IzhikevichCell in time such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = Izhikevich()
>>> l(data) # Returns tuple of (Tensor(10, 5, 2), IzhikevichState)
Parameters

  • p (IzhikevichParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

IzhikevichState

training: bool
class norse.torch.module.IzhikevichCell(spiking_method, **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Module that computes a single Izhikevich neuron-model without recurrence and without time. More specifically it implements one integration step of the following ODE:

\[\begin{align*} \dot{v} &= 0.04v² + 5v + 140 - u + I \dot{u} &= a(bv - u) \end{align*}\]

and

\[\text{if} v = 30 \text{mV, then} v = c \text{and} u = u + d\]
Parameters

spiking_method (IzhikevichSpikingBehavior) – parameters and initial state of the neuron

Example with tonic spiking:
>>> from norse.torch import IzhikevichCell, tonic_spiking
>>> batch_size = 16
>>> cell = IzhikevichCell(tonic_spiking)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = cell(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

IzhikevichState

training: bool
class norse.torch.module.IzhikevichRecurrent(input_size, hidden_size, spiking_method, *args, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrent

A neuron layer that wraps a IzhikevichRecurrentCell in time such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = Izhikevich()
>>> l(data) # Returns tuple of (Tensor(10, 5, 2), IzhikevichState)
Parameters

  • p (IzhikevichParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

IzhikevichRecurrentState

training: bool
class norse.torch.module.IzhikevichRecurrentCell(input_size, hidden_size, spiking_method, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Module that computes a single euler-integration step of an Izhikevich neuron-model with recurrence but without time. More specifically it implements one integration step of the following ODE :

\[\begin{align*} \dot{v} &= 0.04v² + 5v + 140 - u + I \dot{u} &= a(bv - u) \end{align*}\]

and

\[\text{if} v = 30 \text{mV, then} v = c \text{and} u = u + d\]
Example with tonic spiking:
>>> from norse.torch import IzhikevichRecurrentCell, tonic_spiking
>>> batch_size = 16
>>> data = torch.zeros(5, 2) # 5 batches, 2 neurons
>>> l = IzhikevichRecurrentCell(2, 4)
>>> l(data) # Returns tuple of (Tensor(5, 4), IzhikevichState)
Parameters

  • input_size (int) – Size of the input. Also known as the number of input features. Defaults to None

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features. Defaults to None

  • p (IzhikevichParameters) – Parameters of the Izhikevich neuron model.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

IzhikevichRecurrentState

training: bool
class norse.torch.module.LConv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, device=None, dtype=None)[source]

Bases: torch.nn.modules.conv.Conv3d

Implements a 2d-convolution applied pointwise in time. See https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html?highlight=conv2d#torch.nn.Conv2d, for documentation of the arguments, which we will reproduce in part here.

This module expects an additional temporal dimension in the tensor it is passed, that is in the notation in the documentation referenced above, it turns in the simplest case a tensor with input shape \((T, N, C_{ ext{in}}, H, W)\) and output tensor of shape \((T, N, C_{ ext{out}}, H_{ ext{out}}, W_{ ext{out}})\), by applying a 2d convolution operation pointwise along the time-direction, with T denoting the number of time steps.

{groups_note}

The parameters kernel_size, stride, padding, dilation can either be:

  • a single int – in which case the same value is used for the height and width dimension

  • a tuple of two ints – in which case, the first int is used for the height dimension, and the second int for the width dimension

Parameters

  • in_channels (int) – Number of channels in the input image

  • out_channels (int) – Number of channels produced by the convolution

  • kernel_size (int or tuple) – Size of the convolving kernel

  • stride (int or tuple, optional) – Stride of the convolution. Default: 1

  • padding (int, tuple or str, optional) – Padding added to all four sides of the input. Default: 0

  • dilation (int or tuple, optional) – Spacing between kernel elements. Default: 1

  • groups (int, optional) – Number of blocked connections from input channels to output channels. Default: 1

bias: Optional[torch.Tensor]
dilation: Tuple[int, ...]
forward(input_tensor)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

groups: int
kernel_size: Tuple[int, ...]
out_channels: int
output_padding: Tuple[int, ...]
padding: Union[str, Tuple[int, ...]]
padding_mode: str
stride: Tuple[int, ...]
transposed: bool
weight: torch.Tensor
class norse.torch.module.LICell(p=LIParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Cell for a leaky-integrator without recurrence. More specifically it implements a discretized version of the ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

and transition equations

\[i = i + w i_{\text{in}}\]
Parameters

  • p (LIParameters) – parameters of the leaky integrator

  • dt (float) – integration timestep to use

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIState

training: bool
class norse.torch.module.LIF(p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNN

A neuron layer that wraps a LIFCell in time such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIF()
>>> l(data) # Returns tuple of (Tensor(10, 5, 2), LIFState)
Parameters

  • p (LIFParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • sparse (bool) – Whether to apply sparse activation functions (True) or not (False). Defaults to False.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFFeedForwardState

training: bool
class norse.torch.module.LIFAdEx(p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNN

A neuron layer that wraps a recurrent LIFAdExCell in time such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIFAdExLayer(2, 4)
>>> l(data) # Returns tuple of (Tensor(10, 5, 4), LIFExState)
Parameters

  • p (LIFAdExParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFAdExFeedForwardState

training: bool
class norse.torch.module.LIFAdExCell(p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Computes a single euler-integration step of a feed-forward exponential LIF neuron-model without recurrence, adapted from http://www.scholarpedia.org/article/Adaptive_exponential_integrate-and-fire_model. It takes as input the input current as generated by an arbitrary torch module or function. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{a} &= 1/\tau_{\text{ada}} \left( a_{current} (V - v_{\text{leak}}) - a \right) \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[i = i + i_{\text{in}}\]

where \(i_{\text{in}}\) is meant to be the result of applying an arbitrary pytorch module (such as a convolution) to input spikes.

Parameters

Examples

>>> batch_size = 16
>>> lif_ex = LIFAdExCell()
>>> data = torch.randn(batch_size, 20, 30)
>>> output, s0 = lif_ex(data)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(x)[source]
Return type

LIFAdExFeedForwardState

training: bool
class norse.torch.module.LIFAdExFeedForwardState(v: torch.Tensor, i: torch.Tensor, a: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIFAdEx neuron

Parameters

Create new instance of LIFAdExFeedForwardState(v, i, a)

a: torch.Tensor

Alias for field number 2

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.module.LIFAdExParameters(adaptation_current: torch.Tensor = tensor(4), adaptation_spike: torch.Tensor = tensor(0.0200), delta_T: torch.Tensor = tensor(0.5000), tau_ada_inv: torch.Tensor = tensor(2.), tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parametrization of an Adaptive Exponential Leaky Integrate and Fire neuron

Default values from https://github.com/NeuralEnsemble/PyNN/blob/d8056fa956998b031a1c3689a528473ed2bc0265/pyNN/standardmodels/cells.py#L416

Parameters

  • adaptation_current (torch.Tensor) – adaptation coupling parameter in nS

  • adaptation_spike (torch.Tensor) – spike triggered adaptation parameter in nA

  • delta_T (torch.Tensor) – sharpness or speed of the exponential growth in mV

  • tau_syn_inv (torch.Tensor) – inverse adaptation time constant (\(1/\tau_\text{ada}\)) in 1/ms

  • tau_syn_inv – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFAdExParameters(adaptation_current, adaptation_spike, delta_T, tau_ada_inv, tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

adaptation_current: torch.Tensor

Alias for field number 0

adaptation_spike: torch.Tensor

Alias for field number 1

alpha: float

Alias for field number 10

delta_T: torch.Tensor

Alias for field number 2

method: str

Alias for field number 9

tau_ada_inv: torch.Tensor

Alias for field number 3

tau_mem_inv: torch.Tensor

Alias for field number 5

tau_syn_inv: torch.Tensor

Alias for field number 4

v_leak: torch.Tensor

Alias for field number 6

v_reset: torch.Tensor

Alias for field number 8

v_th: torch.Tensor

Alias for field number 7

class norse.torch.module.LIFAdExRecurrent(input_size, hidden_size, p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrent

A neuron layer that wraps a recurrent LIFAdExRecurrentCell in time (with recurrence) such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIFAdExRecurrent(2, 4)
>>> l(data) # Returns tuple of (Tensor(10, 5, 4), LIFAdExState)
Parameters

  • input_size (int) – The number of input neurons

  • hidden_size (int) – The number of hidden neurons

  • p (LIFAdExParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFAdExState

training: bool
class norse.torch.module.LIFAdExRecurrentCell(input_size, hidden_size, p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Computes a single of euler-integration step of a recurrent adaptive exponential LIF neuron-model with recurrence, adapted from http://www.scholarpedia.org/article/Adaptive_exponential_integrate-and-fire_model. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{a} &= 1/\tau_{\text{ada}} \left( a_{current} (V - v_{\text{leak}}) - a \right) \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Examples

>>> batch_size = 16
>>> lif = LIFAdExRecurrentCell(10, 20)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = lif(input)
Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LIFAdExParameters) – Parameters of the LIF neuron model.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFAdExState

training: bool
class norse.torch.module.LIFAdExState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor, a: torch.Tensor)[source]

Bases: tuple

State of a LIFAdEx neuron

Parameters

Create new instance of LIFAdExState(z, v, i, a)

a: torch.Tensor

Alias for field number 3

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.module.LIFCell(p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Module that computes a single euler-integration step of a leaky integrate-and-fire (LIF) neuron-model without recurrence and without time.

More specifically it implements one integration step of the following ODE

\[\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{align*} v &= (1-z) v + z v_{\text{reset}} \end{align*}\]

Example

>>> data = torch.zeros(5, 2) # 5 batches, 2 neurons
>>> l = LIFCell(2, 4)
>>> l(data) # Returns tuple of (Tensor(5, 4), LIFState)
Parameters

  • p (LIFParameters) – Parameters of the LIF neuron model.

  • sparse (bool) – Whether to apply sparse activation functions (True) or not (False). Defaults to False.

  • dt (float) – Time step to use. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFFeedForwardState

training: bool
class norse.torch.module.LIFCorrelation(input_size, hidden_size, p=LIFCorrelationParameters(lif_parameters=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), input_correlation_parameters=CorrelationSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.)), recurrent_correlation_parameters=CorrelationSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.))), dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, input_weights, recurrent_weights, state)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

Return type

Tuple[Tensor, LIFCorrelationState]

training: bool
class norse.torch.module.LIFCorrelationParameters(lif_parameters, input_correlation_parameters, recurrent_correlation_parameters)[source]

Bases: tuple

Create new instance of LIFCorrelationParameters(lif_parameters, input_correlation_parameters, recurrent_correlation_parameters)

input_correlation_parameters: norse.torch.functional.correlation_sensor.CorrelationSensorParameters

Alias for field number 1

lif_parameters: norse.torch.functional.lif.LIFParameters

Alias for field number 0

recurrent_correlation_parameters: norse.torch.functional.correlation_sensor.CorrelationSensorParameters

Alias for field number 2

class norse.torch.module.LIFCorrelationState(lif_state, input_correlation_state, recurrent_correlation_state)[source]

Bases: tuple

Create new instance of LIFCorrelationState(lif_state, input_correlation_state, recurrent_correlation_state)

input_correlation_state: norse.torch.functional.correlation_sensor.CorrelationSensorState

Alias for field number 1

lif_state: norse.torch.functional.lif.LIFState

Alias for field number 0

recurrent_correlation_state: norse.torch.functional.correlation_sensor.CorrelationSensorState

Alias for field number 2

class norse.torch.module.LIFEx(p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNN

A neuron layer that wraps a LIFExCell in time such that the layer keeps track of temporal sequences of spikes. After application, the layer returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIFEx()
>>> l(data) # Returns tuple of (Tensor(10, 5, 2), LIFExState)
Parameters

  • p (LIFExParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable. Defaults to None.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFExFeedForwardState

training: bool
class norse.torch.module.LIFExCell(p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Computes a single euler-integration step of a recurrent exponential LIF neuron-model (without recurrence) adapted from https://neuronaldynamics.epfl.ch/online/Ch5.S2.html. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\\text{reset}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input.

  • hidden_size (int) – Size of the hidden state.

  • p (LIFExParameters) – Parameters of the LIF neuron model.

  • dt (float) – Time step to use.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False.

Examples

>>> batch_size = 16
>>> lif_ex = LIFExCell(10, 20)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = lif_ex(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFExFeedForwardState

training: bool
class norse.torch.module.LIFExFeedForwardState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIFEx neuron

Parameters

Create new instance of LIFExFeedForwardState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.module.LIFExParameters(delta_T: torch.Tensor = tensor(0.5000), tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parametrization of an Exponential Leaky Integrate and Fire neuron

Parameters

  • delta_T (torch.Tensor) – sharpness or speed of the exponential growth in mV

  • tau_syn_inv (torch.Tensor) – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFExParameters(delta_T, tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

alpha: float

Alias for field number 7

delta_T: torch.Tensor

Alias for field number 0

method: str

Alias for field number 6

tau_mem_inv: torch.Tensor

Alias for field number 2

tau_syn_inv: torch.Tensor

Alias for field number 1

v_leak: torch.Tensor

Alias for field number 3

v_reset: torch.Tensor

Alias for field number 5

v_th: torch.Tensor

Alias for field number 4

class norse.torch.module.LIFExRecurrent(input_size, hidden_size, p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrent

A neuron layer that wraps a LIFExRecurrentCell in time such that the layer keeps track of temporal sequences of spikes. After application, the module returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIFExRecurrent(2, 4)
>>> l(data) # Returns tuple of (Tensor(10, 5, 4), LIFExState)
Parameters

  • input_size (int) – The number of input neurons

  • hidden_size (int) – The number of hidden neurons

  • p (LIFExParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable. Defaults to None.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFExState

training: bool
class norse.torch.module.LIFExRecurrentCell(input_size, hidden_size, p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Computes a single euler-integration step of a recurrent exponential LIFEx neuron-model (with recurrence) adapted from https://neuronaldynamics.epfl.ch/online/Ch5.S2.html. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input.

  • hidden_size (int) – Size of the hidden state.

  • p (LIFExParameters) – Parameters of the LIF neuron model.

  • dt (float) – Time step to use.

  • a (bool) – Allow self-connections in the recurrence? Defaults to False.

Examples

>>> batch_size = 16
>>> lif_ex = LIFExRecurrentCell(10, 20)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = lif_ex(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFExState

training: bool
class norse.torch.module.LIFExState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a LIFEx neuron

Parameters

Create new instance of LIFExState(z, v, i)

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.module.LIFFeedForwardState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIF neuron

Parameters

Create new instance of LIFFeedForwardState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.module.LIFMCRecurrentCell(input_size, hidden_size, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), g_coupling=None, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Computes a single euler-integration step of a LIF multi-compartment neuron-model.

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} \ - g_{\text{coupling}} v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • g_coupling (torch.Tensor) – conductances between the neuron compartments

  • p (LIFParameters) – neuron parameters

  • dt (float) – Integration timestep to use

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, state=None)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

Return type

Tuple[Tensor, LIFState]

initial_state(input_tensor)[source]
Return type

LIFState

training: bool
class norse.torch.module.LIFMCRefracRecurrentCell(input_size, hidden_size, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), g_coupling=None, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, state=None)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

Return type

Tuple[Tensor, LIFRefracState]

initial_state(input_tensor)[source]
Return type

LIFRefracState

training: bool
class norse.torch.module.LIFParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = tensor(100.))[source]

Bases: tuple

Parametrization of a LIF neuron

Parameters

  • tau_syn_inv (torch.Tensor) – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFParameters(tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

alpha: float

Alias for field number 6

method: str

Alias for field number 5

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 2

v_reset: torch.Tensor

Alias for field number 4

v_th: torch.Tensor

Alias for field number 3

class norse.torch.module.LIFRecurrent(input_size, hidden_size, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrent

A neuron layer that wraps a LIFRecurrentCell in time such that the layer keeps track of temporal sequences of spikes. After application, the module returns a tuple containing

(spikes from all timesteps, state from the last timestep).

Example

>>> data = torch.zeros(10, 5, 2) # 10 timesteps, 5 batches, 2 neurons
>>> l = LIFRecurrent(2, 4)
>>> l(data) # Returns tuple of (Tensor(10, 5, 4), LIFState)
Parameters

  • input_size (int) – The number of input neurons

  • hidden_size (int) – The number of hidden neurons

  • p (LIFParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • sparse (bool) – Whether to apply sparse activation functions (True) or not (False). Defaults to False.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFState

training: bool
class norse.torch.module.LIFRecurrentCell(input_size, hidden_size, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Module that computes a single euler-integration step of a leaky integrate-and-fire (LIF) neuron-model with recurrence but without time. More specifically it implements one integration step of the following ODE

\[\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{align*} v &= (1-z) v + z v_{\text{reset}} \ i &= i + w_{\text{input}} z_{\text{in}} \ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Example

>>> data = torch.zeros(5, 2) # 5 batches, 2 neurons
>>> l = LIFRecurrentCell(2, 4)
>>> l(data) # Returns tuple of (Tensor(5, 4), LIFState)
Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LIFParameters) – Parameters of the LIF neuron model.

  • sparse (bool) – Whether to apply sparse activation functions (True) or not (False). Defaults to False.

  • input_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • recurrent_weights (torch.Tensor) – Weights used for input tensors. Defaults to a random matrix normalized to the number of hidden neurons.

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False. Will also remove autapses in custom recurrent weights, if set above.

  • dt (float) – Time step to use.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFState

training: bool
class norse.torch.module.LIFRefracCell(p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Module that computes a single euler-integration step of a LIF neuron-model with absolute refractory period without recurrence. More specifically it implements one integration step of the following ODE.

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (1-\Theta(\rho)) (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{\rho} &= -1/\tau_{\text{refrac}} \Theta(\rho) \end{align*}\end{split}\]

together with the jump condition

\[\begin{split}\begin{align*} z &= \Theta(v - v_{\text{th}}) \\ z_r &= \Theta(-\rho) \end{align*}\end{split}\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ \rho &= \rho + z_r \rho_{\text{reset}} \end{align*}\end{split}\]
Parameters

Examples

>>> batch_size = 16
>>> lif = LIFRefracCell()
>>> input = torch.randn(batch_size, 20, 30)
>>> output, s0 = lif(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFRefracFeedForwardState

training: bool
class norse.torch.module.LIFRefracFeedForwardState(lif: norse.torch.functional.lif.LIFFeedForwardState, rho: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIF neuron with absolute refractory period.

Parameters

Create new instance of LIFRefracFeedForwardState(lif, rho)

lif: norse.torch.functional.lif.LIFFeedForwardState

Alias for field number 0

rho: torch.Tensor

Alias for field number 1

class norse.torch.module.LIFRefracParameters(lif: norse.torch.functional.lif.LIFParameters = LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset: torch.Tensor = tensor(5.))[source]

Bases: tuple

Parameters of a LIF neuron with absolute refractory period.

Parameters

  • lif (LIFParameters) – parameters of the LIF neuron integration

  • rho (torch.Tensor) – refractory state (count towards zero)

Create new instance of LIFRefracParameters(lif, rho_reset)

lif: norse.torch.functional.lif.LIFParameters

Alias for field number 0

rho_reset: torch.Tensor

Alias for field number 1

class norse.torch.module.LIFRefracRecurrentCell(input_size, hidden_size, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Module that computes a single euler-integration step of a LIF neuron-model with absolute refractory period. More specifically it implements one integration step of the following ODE.

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (1-\Theta(\rho)) (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{\rho} &= -1/\tau_{\text{refrac}} \Theta(\rho) \end{align*}\end{split}\]

together with the jump condition

\[\begin{split}\begin{align*} z &= \Theta(v - v_{\text{th}}) \\ z_r &= \Theta(-\rho) \end{align*}\end{split}\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \\ \rho &= \rho + z_r \rho_{\text{reset}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LIFRefracParameters) – parameters of the lif neuron

  • dt (float) – Integration timestep to use

  • autapses (bool) – Allow self-connections in the recurrence? Defaults to False.

Examples

>>> batch_size = 16
>>> lif = LIFRefracRecurrentCell(10, 20)
>>> input = torch.randn(batch_size, 10)
>>> output, s0 = lif(input)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LIFRefracState

training: bool
class norse.torch.module.LIFRefracState(lif: norse.torch.functional.lif.LIFState, rho: torch.Tensor)[source]

Bases: tuple

State of a LIF neuron with absolute refractory period.

Parameters

  • lif (LIFState) – state of the LIF neuron integration

  • rho (torch.Tensor) – refractory state (count towards zero)

Create new instance of LIFRefracState(lif, rho)

lif: norse.torch.functional.lif.LIFState

Alias for field number 0

rho: torch.Tensor

Alias for field number 1

class norse.torch.module.LIFState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a LIF neuron

Parameters

Create new instance of LIFState(z, v, i)

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.module.LILinearCell(input_size, hidden_size, p=LIParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.)), dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Cell for a leaky-integrator with an additional linear weighting. More specifically it implements a discretized version of the ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

and transition equations

\[i = i + w i_{\text{in}}\]
Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LIParameters) – parameters of the leaky integrator

  • dt (float) – integration timestep to use

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, state=None)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

Return type

Tuple[Tensor, LIState]

training: bool
class norse.torch.module.LIParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.))[source]

Bases: tuple

Parameters of a leaky integrator

Parameters

Create new instance of LIParameters(tau_syn_inv, tau_mem_inv, v_leak)

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 2

class norse.torch.module.LIState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a leaky-integrator

Parameters

Create new instance of LIState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.module.LSNN(p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), adjoint=False, **kwargs)[source]

Bases: norse.torch.module.snn.SNN

A Long short-term memory neuron module without recurrence adapted from https://arxiv.org/abs/1803.09574

Usage:
>>> from norse.torch import LSNN
>>> layer = LSNN()
>>> data  = torch.zeros(5, 2)
>>> output, state = layer.forward(data)
Parameters

  • p (LSNNParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LSNNFeedForwardState

training: bool
class norse.torch.module.LSNNCell(p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), adjoint=False, **kwargs)[source]

Bases: norse.torch.module.snn.SNNCell

Euler integration cell for LIF Neuron with threshold adaptation without recurrence. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\\text{syn}} i \\ \dot{b} &= -1/\tau_{b} b \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}} + b)\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + \text{input} \\ b &= b + \beta z \end{align*}\end{split}\]
Parameters

  • p (torch.nn.Module) – parameters of the lsnn unit

  • p – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LSNNFeedForwardState

training: bool
class norse.torch.module.LSNNFeedForwardState(v: torch.Tensor, i: torch.Tensor, b: torch.Tensor)[source]

Bases: tuple

Integration state kept for a lsnn module

Parameters

Create new instance of LSNNFeedForwardState(v, i, b)

b: torch.Tensor

Alias for field number 2

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.module.LSNNParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), tau_adapt_inv: torch.Tensor = tensor(0.0012), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), beta: torch.Tensor = tensor(1.8000), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parameters of an LSNN neuron

Parameters

Create new instance of LSNNParameters(tau_syn_inv, tau_mem_inv, tau_adapt_inv, v_leak, v_th, v_reset, beta, method, alpha)

alpha: float

Alias for field number 8

beta: torch.Tensor

Alias for field number 6

method: str

Alias for field number 7

tau_adapt_inv: torch.Tensor

Alias for field number 2

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 3

v_reset: torch.Tensor

Alias for field number 5

v_th: torch.Tensor

Alias for field number 4

class norse.torch.module.LSNNRecurrent(input_size, hidden_size, p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), adjoint=False, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrent

A Long short-term memory neuron module wit recurrence adapted from https://arxiv.org/abs/1803.09574

Usage:
>>> from norse.torch.module import LSNNRecurrent
>>> layer = LSNNRecurrent(2, 10)          // Shape 2 -> 10
>>> data  = torch.zeros(2, 5, 2)          // Arbitrary data
>>> output, state = layer.forward(data)   // Out: (2, 5, 10)
Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LSNNParameters) – The neuron parameters as a torch Module, which allows the module to configure neuron parameters as optimizable.

  • dt (float) – Time step to use in integration. Defaults to 0.001.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LSNNState

training: bool
class norse.torch.module.LSNNRecurrentCell(input_size, hidden_size, p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), adjoint=False, **kwargs)[source]

Bases: norse.torch.module.snn.SNNRecurrentCell

Module that computes a single euler-integration step of a LSNN neuron-model with recurrence. More specifically it implements one integration step of the following ODE

\[\begin{split}\\begin{align*} \dot{v} &= 1/\\tau_{\\text{mem}} (v_{\\text{leak}} - v + i) \\\\ \dot{i} &= -1/\\tau_{\\text{syn}} i \\\\ \dot{b} &= -1/\\tau_{b} b \end{align*}\end{split}\]

together with the jump condition

\[\begin{split}z = \Theta(v - v_{\\text{th}} + b)\end{split}\]

and transition equations

\[\begin{split}\\begin{align*} v &= (1-z) v + z v_{\\text{reset}} \\\\ i &= i + w_{\\text{input}} z_{\\text{in}} \\\\ i &= i + w_{\\text{rec}} z_{\\text{rec}} \\\\ b &= b + \\beta z \end{align*}\end{split}\]

where \(z_{\\text{rec}}\) and \(z_{\\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_size (int) – Size of the input. Also known as the number of input features.

  • hidden_size (int) – Size of the hidden state. Also known as the number of input features.

  • p (LSNNParameters) – parameters of the lsnn unit

  • dt (float) – Integration timestep to use

Initializes internal Module state, shared by both nn.Module and ScriptModule.

initial_state(input_tensor)[source]
Return type

LSNNState

training: bool
class norse.torch.module.LSNNState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor, b: torch.Tensor)[source]

Bases: tuple

State of an LSNN neuron

Parameters

Create new instance of LSNNState(z, v, i, b)

b: torch.Tensor

Alias for field number 3

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.module.Lift(module)[source]

Bases: torch.nn.modules.module.Module

Lift applies a given torch.nn.Module over

a temporal sequence. In other words this module applies the given torch.nn.Module N times, where N is the outer dimension in the provided tensor.

Parameters

module (Module) – Module to apply

Examples

>>> batch_size = 16
>>> seq_length = 1000
>>> in_channels = 64
>>> out_channels = 32
>>> conv2d = Lift(torch.nn.Conv2d(in_channels, out_channels, 5, 1))
>>> data = torch.randn(seq_length, batch_size, 20, 30)
>>> output = conv2d(data)

>>> data = torch.randn(seq_length, batch_size, in_channels, 20, 30)
>>> module = torch.nn.Sequential(
>>>     Lift(torch.nn.Conv2d(in_channels, out_channels, 5, 1)),
>>>     LIF(),
>>> )
>>> output, _ = module(data)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(x)[source]

Apply the module over the input along the 0-th (time) dimension and accumulate the outputs in an output tensor.

Parameters

x (Union[Tensor, Tuple[Tensor, Tensor]]) – Union[torch.Tensor, Tuple[torch.Tensor, torch.Tensor]]

Note

If the input is a tuple of two tensors, the second tuple entry will be ignored.

Return type

Tensor

training: bool
class norse.torch.module.PoissonEncoder(seq_length, f_max=100, dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Encodes a tensor of input values, which are assumed to be in the range [0,1] into a tensor of one dimension higher of binary values, which represent input spikes.

Parameters

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • f_max (float) – Maximal frequency (in Hertz) which will be emitted.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

forward(x)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.PopulationEncoder(out_features, scale=None, kernel=<function gaussian_rbf>, distance_function=<function euclidean_distance>)[source]

Bases: torch.nn.modules.module.Module

Encodes a set of input values into population codes, such that each singular input value is represented by a list of numbers (typically calculated by a radial basis kernel), whose length is equal to the out_features.

Population encoding can be visualised by imagining a number of neurons in a list, whose activity increases if a number gets close to its “receptive field”.

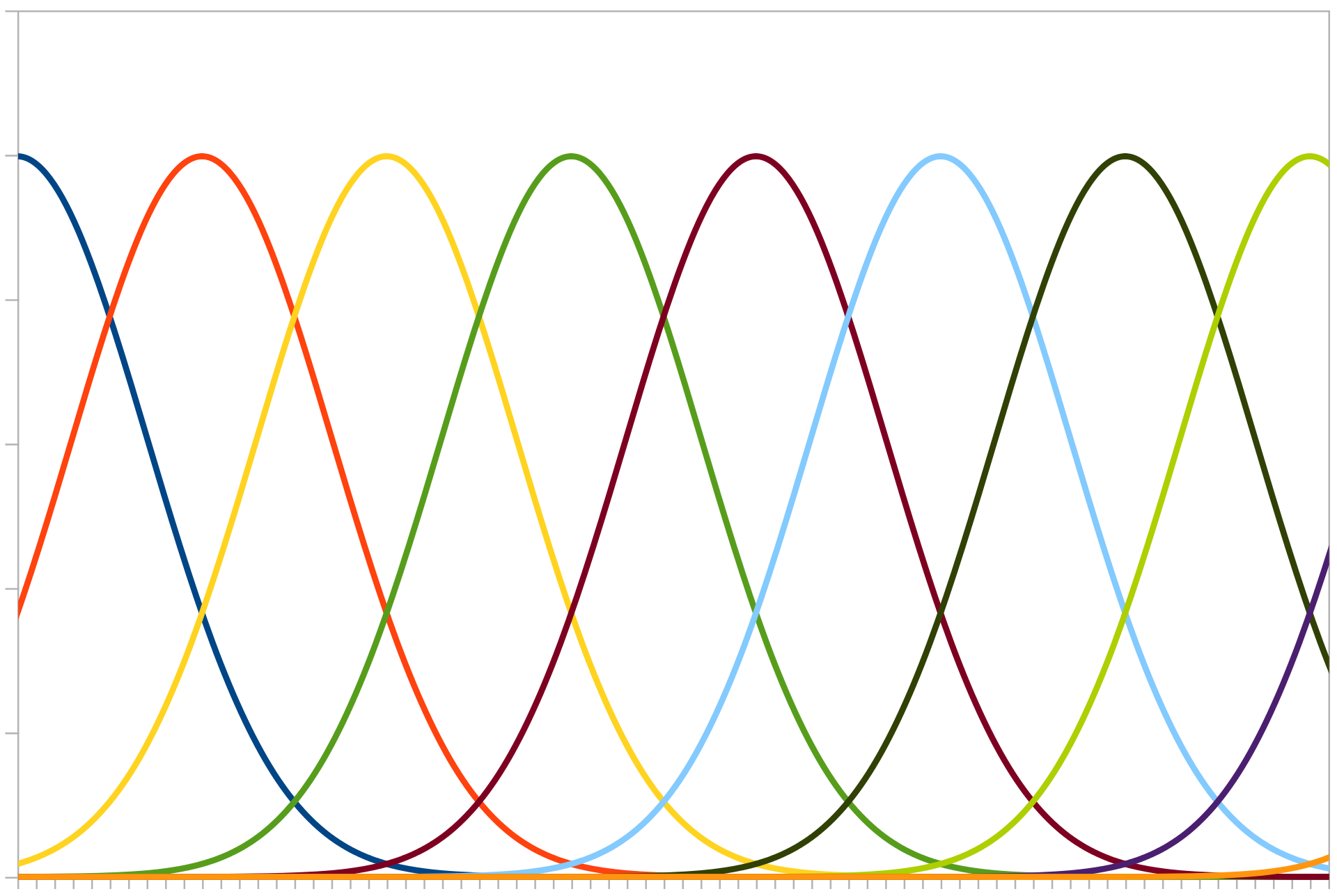
https://upload.wikimedia.org/wikipedia/commons/thumb/a/a1/PopulationCode.svg/1920px-PopulationCode.svg.png

Gaussian curves representing different neuron “receptive fields”. Image credit: Andrew K. Richardson.

super(PopulationEncoder, self).__init__()mons.wikimedia.org/wiki/File:PopulationCode.svg

Example

>>> data = torch.as_tensor([0, 0.5, 1])
>>> out_features = 3
>>> PopulationEncoder(out_features).forward(data)
tensor([[1.0000, 0.8825, 0.6065],
        [0.8825, 1.0000, 0.8825],
        [0.6065, 0.8825, 1.0000]])
Parameters

  • out_features (int) – The number of output per input value

  • scale (torch.Tensor) – The scaling factor for the kernels. Defaults to the maximum value of the input. Can also be set for each individual sample.

  • kernel (Callable[[Tensor], Tensor]) – A function that takes two inputs and returns a tensor. The two inputs represent the center value (which changes for each index in the output tensor) and the actual data value to encode respectively.z Defaults to gaussian radial basis kernel function.

  • distance_function (Callable[[Tensor, Tensor], Tensor]) – A function that calculates the distance between two numbers. Defaults to euclidean.

forward(input_tensor)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.RegularizationCell(accumulator=<function spike_accumulator>, state=None)[source]

Bases: torch.nn.modules.module.Module

A regularisation cell that accumulates some state (for instance number of spikes) for each forward step, which can later be applied to a loss term.

Example

>>> import torch
>>> from norse.torch.module import lif, regularization
>>> cell = lif.LIFCell(2, 4) # 2 -> 4
>>> r = regularization.RegularizationCell() # Defaults to spike counting
>>> data = torch.ones(5, 2)  # Batch size of 5
>>> z, s = cell(data)
>>> z, regularization_term = r(z, s)
>>> ...
>>> loss = ... + 1e-3 * regularization_term
Parameters

  • accumulator (Accumulator) – The accumulator that aggregates some data (such as spikes) that can later be included in an error term.

  • state (Optional[T]) – The regularization state to be aggregated to of any type T. Defaults to None.

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(z, s)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.SequentialState(*args)[source]

Bases: torch.nn.modules.container.Sequential

A sequential model that works like PyTorch’s Sequential with the addition that it handles neuron states.

Parameters

args (*torch.nn.Module) – A list of modules to sequentially apply in the forward pass

Example

>>> import torch
>>> import norse.torch as snn
>>> data = torch.ones(1, 16, 8, 4)         # Single timestep
>>> model = snn.SequentialState(
>>>   snn.Lift(torch.nn.Conv2d(16, 8, 3)), # (1, 8, 6, 2)
>>>   torch.nn.Flatten(2),                 # (1, 8, 12)
>>>   snn.LIFRecurrent(12, 6),             # (1, 8, 6)
>>>   snn.LIFRecurrent(6, 1)               # (1, 8, 1)
>>> )
>>> model(data)
Example with recurrent layers:
>>> import torch
>>> import norse.torch as snn
>>> data = torch.ones(1, 16, 8, 4)         # Single timestep
>>> model = snn.SequentialState(
>>>   snn.Lift(torch.nn.Conv2d(16, 8, 3)), # (1, 8, 6, 2)
>>>   torch.nn.Flatten(2),                 # (1, 8, 12)
>>>   snn.LSNNRecurrent(12, 6),            # (1, 8, 6)
>>>   torch.nn.RNN(6, 4, 2),               # (1, 6, 4) with 2 recurrent layers
>>>   snn.LIFRecurrent(4, 1)               # (1, 4, 1)
>>> )
>>> model(data)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_tensor, state=None)[source]

Feeds the input to the modules with the given state-list. If the state is None, the initial state is set to None for each of the modules.

Parameters

  • input_tensor (Tensor) – The input tensor too feed into the first module

  • state (Optional[list]) – Either a list of states for each module or None. If None, the modules will initialise their own default state

Returns

A tuple of (output tensor, state list)

register_forward_state_hooks(forward_hook)[source]

Registers hooks for all state*ful* layers.

Hooks can be removed by calling :meth:`remove_state_hooks`_.

Parameters

  • child_hook (Callable) – The hook applied to all children everytime they produce an output

  • pre_hook (Optional[Callable]) – An optional hook for the SequentialState module, executed before the input is propagated to the children.

Example

>>> import norse.torch as snn
>>> def my_hook(module, input, output):
>>>     ...
>>> module = snn.SequentialState(...)
>>> module.register_forward_state_hook(my_hook)
>>> module(...)
remove_forward_state_hooks()[source]

Disables the forward state hooks, registered in :meth:`register_forward_state_hooks`_.

training: bool
class norse.torch.module.SignedPoissonEncoder(seq_length, f_max=100, dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Encodes a tensor of input values, which are assumed to be in the range [-1,1] into a tensor of one dimension higher of values in {-1,0,1}, which represent signed input spikes.

Parameters

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • f_max (float) – Maximal frequency (in Hertz) which will be emitted.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

forward(x)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.SpikeLatencyEncoder[source]

Bases: torch.nn.modules.module.Module

For all neurons, remove all but the first spike. This encoding basically measures the time it takes for a neuron to spike first. Assuming that the inputs are constant, this makes sense in that strong inputs spikes fast.

See R. Van Rullen & S. J. Thorpe (2001): Rate Coding Versus Temporal Order Coding: What the Retinal Ganglion Cells Tell the Visual Cortex.

Spikes are identified by their unique position in the input array.

Example

>>> data = torch.as_tensor([[0, 1, 1], [1, 1, 1]])
>>> encoder = torch.nn.Sequential(
                ConstantCurrentLIFEncoder()
                SpikeLatencyEncoder()
                )
>>> encoder(data)
tensor([[0, 1, 1],
        [1, 0, 0]])

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_spikes)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool
class norse.torch.module.SpikeLatencyLIFEncoder(seq_length, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Bases: torch.nn.modules.module.Module

Encodes an input value by the time the first spike occurs. Similar to the ConstantCurrentLIFEncoder, but the LIF can be thought to have an infinite refractory period.

Parameters

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • p (LIFParameters) – Parameters of the LIF neuron model.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

Initializes internal Module state, shared by both nn.Module and ScriptModule.

forward(input_current)[source]

Defines the computation performed at every call.

Should be overridden by all subclasses.

Note

Although the recipe for forward pass needs to be defined within this function, one should call the Module instance afterwards instead of this since the former takes care of running the registered hooks while the latter silently ignores them.

training: bool