norse.torch.functional package

Stateless spiking neural network components.

class norse.torch.functional.CobaLIFFeedForwardState(v: torch.Tensor, g_e: torch.Tensor, g_i: torch.Tensor)[source]

Bases: tuple

State of a conductance based feed forward LIF neuron.

Parameters

Create new instance of CobaLIFFeedForwardState(v, g_e, g_i)

g_e: torch.Tensor

Alias for field number 1

g_i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.CobaLIFParameters(tau_syn_exc_inv: torch.Tensor = tensor(0.2000), tau_syn_inh_inv: torch.Tensor = tensor(0.2000), c_m_inv: torch.Tensor = tensor(5.), g_l: torch.Tensor = tensor(0.2500), e_rev_I: torch.Tensor = tensor(- 100), e_rev_E: torch.Tensor = tensor(60), v_rest: torch.Tensor = tensor(- 20), v_reset: torch.Tensor = tensor(- 70), v_thresh: torch.Tensor = tensor(- 10), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parameters of conductance based LIF neuron.

Parameters

  • tau_syn_exc_inv (torch.Tensor) – inverse excitatory synaptic input time constant

  • tau_syn_inh_inv (torch.Tensor) – inverse inhibitory synaptic input time constant

  • c_m_inv (torch.Tensor) – inverse membrane capacitance

  • g_l (torch.Tensor) – leak conductance

  • e_rev_I (torch.Tensor) – inhibitory reversal potential

  • e_rev_E (torch.Tensor) – excitatory reversal potential

  • v_rest (torch.Tensor) – rest membrane potential

  • v_reset (torch.Tensor) – reset membrane potential

  • v_thresh (torch.Tensor) – threshold membrane potential

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of CobaLIFParameters(tau_syn_exc_inv, tau_syn_inh_inv, c_m_inv, g_l, e_rev_I, e_rev_E, v_rest, v_reset, v_thresh, method, alpha)

alpha: float

Alias for field number 10

c_m_inv: torch.Tensor

Alias for field number 2

e_rev_E: torch.Tensor

Alias for field number 5

e_rev_I: torch.Tensor

Alias for field number 4

g_l: torch.Tensor

Alias for field number 3

method: str

Alias for field number 9

tau_syn_exc_inv: torch.Tensor

Alias for field number 0

tau_syn_inh_inv: torch.Tensor

Alias for field number 1

v_reset: torch.Tensor

Alias for field number 7

v_rest: torch.Tensor

Alias for field number 6

v_thresh: torch.Tensor

Alias for field number 8

class norse.torch.functional.CobaLIFState(z: torch.Tensor, v: torch.Tensor, g_e: torch.Tensor, g_i: torch.Tensor)[source]

Bases: tuple

State of a conductance based LIF neuron.

Parameters

Create new instance of CobaLIFState(z, v, g_e, g_i)

g_e: torch.Tensor

Alias for field number 2

g_i: torch.Tensor

Alias for field number 3

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.CorrelationSensorParameters(eta_p, eta_m, tau_ac_inv, tau_c_inv)[source]

Bases: tuple

Create new instance of CorrelationSensorParameters(eta_p, eta_m, tau_ac_inv, tau_c_inv)

eta_m: torch.Tensor

Alias for field number 1

eta_p: torch.Tensor

Alias for field number 0

tau_ac_inv: torch.Tensor

Alias for field number 2

tau_c_inv: torch.Tensor

Alias for field number 3

class norse.torch.functional.CorrelationSensorState(post_pre, correlation_trace, anti_correlation_trace)[source]

Bases: tuple

Create new instance of CorrelationSensorState(post_pre, correlation_trace, anti_correlation_trace)

anti_correlation_trace: torch.Tensor

Alias for field number 2

correlation_trace: torch.Tensor

Alias for field number 1

post_pre: torch.Tensor

Alias for field number 0

class norse.torch.functional.IzhikevichParameters(a: float, b: float, c: float, d: float, sq: float = 0.04, mn: float = 5, bias: float = 140, v_th: float = 30, tau_inv: float = 250, method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parametrization of av Izhikevich neuron :param a: time scale of the recovery variable u. Smaller values result in slower recovery in 1/ms :type a: float :param b: sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential v. Greater values couple v and u more strongly resulting in possible subthreshold oscillations and low-threshold spiking dynamics :type b: float :param c: after-spike reset value of the membrane potential in mV :type c: float :param d: after-spike reset of the recovery variable u caused by slow high-threshold Na+ and K+ conductances in mV :type d: float :param sq: constant of the v squared variable in mV/ms :type sq: float :param mn: constant of the v variable in 1/ms :type mn: float :param bias: bias constant in mV/ms :type bias: float :param v_th: threshold potential in mV :type v_th: torch.Tensor :param tau_inv: inverse time constant in 1/ms :type tau_inv: float :param method: method to determine the spike threshold

(relevant for surrogate gradients)

Parameters

alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of IzhikevichParameters(a, b, c, d, sq, mn, bias, v_th, tau_inv, method, alpha)

a: float

Alias for field number 0

alpha: float

Alias for field number 10

b: float

Alias for field number 1

bias: float

Alias for field number 6

c: float

Alias for field number 2

d: float

Alias for field number 3

method: str

Alias for field number 9

mn: float

Alias for field number 5

sq: float

Alias for field number 4

tau_inv: float

Alias for field number 8

v_th: float

Alias for field number 7

class norse.torch.functional.IzhikevichRecurrentState(z: torch.Tensor, v: torch.Tensor, u: torch.Tensor)[source]

Bases: tuple

State of a Izhikevich neuron :param v: membrane potential :type v: torch.Tensor :param u: membrane recovery variable :type u: torch.Tensor

Create new instance of IzhikevichRecurrentState(z, v, u)

u: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.IzhikevichSpikingBehavior(p: norse.torch.functional.izhikevich.IzhikevichParameters, s: norse.torch.functional.izhikevich.IzhikevichState)[source]

Bases: tuple

Spiking behavior of a Izhikevich neuron :param p: parameters of the Izhikevich neuron model :type p: IzhikevichParameters :param s: state of the Izhikevich neuron model :type s: IzhikevichState

Create new instance of IzhikevichSpikingBehavior(p, s)

p: norse.torch.functional.izhikevich.IzhikevichParameters

Alias for field number 0

s: norse.torch.functional.izhikevich.IzhikevichState

Alias for field number 1

class norse.torch.functional.IzhikevichState(v: torch.Tensor, u: torch.Tensor)[source]

Bases: tuple

State of a Izhikevich neuron :param v: membrane potential :type v: torch.Tensor :param u: membrane recovery variable :type u: torch.Tensor

Create new instance of IzhikevichState(v, u)

u: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFAdExFeedForwardState(v: torch.Tensor, i: torch.Tensor, a: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIFAdEx neuron

Parameters

Create new instance of LIFAdExFeedForwardState(v, i, a)

a: torch.Tensor

Alias for field number 2

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFAdExParameters(adaptation_current: torch.Tensor = tensor(4), adaptation_spike: torch.Tensor = tensor(0.0200), delta_T: torch.Tensor = tensor(0.5000), tau_ada_inv: torch.Tensor = tensor(2.), tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parametrization of an Adaptive Exponential Leaky Integrate and Fire neuron

Default values from https://github.com/NeuralEnsemble/PyNN/blob/d8056fa956998b031a1c3689a528473ed2bc0265/pyNN/standardmodels/cells.py#L416

Parameters

  • adaptation_current (torch.Tensor) – adaptation coupling parameter in nS

  • adaptation_spike (torch.Tensor) – spike triggered adaptation parameter in nA

  • delta_T (torch.Tensor) – sharpness or speed of the exponential growth in mV

  • tau_syn_inv (torch.Tensor) – inverse adaptation time constant (\(1/\tau_\text{ada}\)) in 1/ms

  • tau_syn_inv – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFAdExParameters(adaptation_current, adaptation_spike, delta_T, tau_ada_inv, tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

adaptation_current: torch.Tensor

Alias for field number 0

adaptation_spike: torch.Tensor

Alias for field number 1

alpha: float

Alias for field number 10

delta_T: torch.Tensor

Alias for field number 2

method: str

Alias for field number 9

tau_ada_inv: torch.Tensor

Alias for field number 3

tau_mem_inv: torch.Tensor

Alias for field number 5

tau_syn_inv: torch.Tensor

Alias for field number 4

v_leak: torch.Tensor

Alias for field number 6

v_reset: torch.Tensor

Alias for field number 8

v_th: torch.Tensor

Alias for field number 7

class norse.torch.functional.LIFAdExState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor, a: torch.Tensor)[source]

Bases: tuple

State of a LIFAdEx neuron

Parameters

Create new instance of LIFAdExState(z, v, i, a)

a: torch.Tensor

Alias for field number 3

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFCorrelationParameters(lif_parameters, input_correlation_parameters, recurrent_correlation_parameters)[source]

Bases: tuple

Create new instance of LIFCorrelationParameters(lif_parameters, input_correlation_parameters, recurrent_correlation_parameters)

input_correlation_parameters: norse.torch.functional.correlation_sensor.CorrelationSensorParameters

Alias for field number 1

lif_parameters: norse.torch.functional.lif.LIFParameters

Alias for field number 0

recurrent_correlation_parameters: norse.torch.functional.correlation_sensor.CorrelationSensorParameters

Alias for field number 2

class norse.torch.functional.LIFCorrelationState(lif_state, input_correlation_state, recurrent_correlation_state)[source]

Bases: tuple

Create new instance of LIFCorrelationState(lif_state, input_correlation_state, recurrent_correlation_state)

input_correlation_state: norse.torch.functional.correlation_sensor.CorrelationSensorState

Alias for field number 1

lif_state: norse.torch.functional.lif.LIFState

Alias for field number 0

recurrent_correlation_state: norse.torch.functional.correlation_sensor.CorrelationSensorState

Alias for field number 2

class norse.torch.functional.LIFExFeedForwardState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIFEx neuron

Parameters

Create new instance of LIFExFeedForwardState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFExParameters(delta_T: torch.Tensor = tensor(0.5000), tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parametrization of an Exponential Leaky Integrate and Fire neuron

Parameters

  • delta_T (torch.Tensor) – sharpness or speed of the exponential growth in mV

  • tau_syn_inv (torch.Tensor) – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFExParameters(delta_T, tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

alpha: float

Alias for field number 7

delta_T: torch.Tensor

Alias for field number 0

method: str

Alias for field number 6

tau_mem_inv: torch.Tensor

Alias for field number 2

tau_syn_inv: torch.Tensor

Alias for field number 1

v_leak: torch.Tensor

Alias for field number 3

v_reset: torch.Tensor

Alias for field number 5

v_th: torch.Tensor

Alias for field number 4

class norse.torch.functional.LIFExState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a LIFEx neuron

Parameters

Create new instance of LIFExState(z, v, i)

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFFeedForwardState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIF neuron

Parameters

Create new instance of LIFFeedForwardState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIFParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), method: str = 'super', alpha: float = tensor(100.))[source]

Bases: tuple

Parametrization of a LIF neuron

Parameters

  • tau_syn_inv (torch.Tensor) – inverse synaptic time constant (\(1/\tau_\text{syn}\)) in 1/ms

  • tau_mem_inv (torch.Tensor) – inverse membrane time constant (\(1/\tau_\text{mem}\)) in 1/ms

  • v_leak (torch.Tensor) – leak potential in mV

  • v_th (torch.Tensor) – threshold potential in mV

  • v_reset (torch.Tensor) – reset potential in mV

  • method (str) – method to determine the spike threshold (relevant for surrogate gradients)

  • alpha (float) – hyper parameter to use in surrogate gradient computation

Create new instance of LIFParameters(tau_syn_inv, tau_mem_inv, v_leak, v_th, v_reset, method, alpha)

alpha: float

Alias for field number 6

method: str

Alias for field number 5

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 2

v_reset: torch.Tensor

Alias for field number 4

v_th: torch.Tensor

Alias for field number 3

class norse.torch.functional.LIFRefracFeedForwardState(lif: norse.torch.functional.lif.LIFFeedForwardState, rho: torch.Tensor)[source]

Bases: tuple

State of a feed forward LIF neuron with absolute refractory period.

Parameters

Create new instance of LIFRefracFeedForwardState(lif, rho)

lif: norse.torch.functional.lif.LIFFeedForwardState

Alias for field number 0

rho: torch.Tensor

Alias for field number 1

class norse.torch.functional.LIFRefracParameters(lif: norse.torch.functional.lif.LIFParameters = LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset: torch.Tensor = tensor(5.))[source]

Bases: tuple

Parameters of a LIF neuron with absolute refractory period.

Parameters

  • lif (LIFParameters) – parameters of the LIF neuron integration

  • rho (torch.Tensor) – refractory state (count towards zero)

Create new instance of LIFRefracParameters(lif, rho_reset)

lif: norse.torch.functional.lif.LIFParameters

Alias for field number 0

rho_reset: torch.Tensor

Alias for field number 1

class norse.torch.functional.LIFRefracState(lif: norse.torch.functional.lif.LIFState, rho: torch.Tensor)[source]

Bases: tuple

State of a LIF neuron with absolute refractory period.

Parameters

  • lif (LIFState) – state of the LIF neuron integration

  • rho (torch.Tensor) – refractory state (count towards zero)

Create new instance of LIFRefracState(lif, rho)

lif: norse.torch.functional.lif.LIFState

Alias for field number 0

rho: torch.Tensor

Alias for field number 1

class norse.torch.functional.LIFState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a LIF neuron

Parameters

Create new instance of LIFState(z, v, i)

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.LIParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), v_leak: torch.Tensor = tensor(0.))[source]

Bases: tuple

Parameters of a leaky integrator

Parameters

Create new instance of LIParameters(tau_syn_inv, tau_mem_inv, v_leak)

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 2

class norse.torch.functional.LIState(v: torch.Tensor, i: torch.Tensor)[source]

Bases: tuple

State of a leaky-integrator

Parameters

Create new instance of LIState(v, i)

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LSNNFeedForwardState(v: torch.Tensor, i: torch.Tensor, b: torch.Tensor)[source]

Bases: tuple

Integration state kept for a lsnn module

Parameters

Create new instance of LSNNFeedForwardState(v, i, b)

b: torch.Tensor

Alias for field number 2

i: torch.Tensor

Alias for field number 1

v: torch.Tensor

Alias for field number 0

class norse.torch.functional.LSNNParameters(tau_syn_inv: torch.Tensor = tensor(200.), tau_mem_inv: torch.Tensor = tensor(100.), tau_adapt_inv: torch.Tensor = tensor(0.0012), v_leak: torch.Tensor = tensor(0.), v_th: torch.Tensor = tensor(1.), v_reset: torch.Tensor = tensor(0.), beta: torch.Tensor = tensor(1.8000), method: str = 'super', alpha: float = 100.0)[source]

Bases: tuple

Parameters of an LSNN neuron

Parameters

Create new instance of LSNNParameters(tau_syn_inv, tau_mem_inv, tau_adapt_inv, v_leak, v_th, v_reset, beta, method, alpha)

alpha: float

Alias for field number 8

beta: torch.Tensor

Alias for field number 6

method: str

Alias for field number 7

tau_adapt_inv: torch.Tensor

Alias for field number 2

tau_mem_inv: torch.Tensor

Alias for field number 1

tau_syn_inv: torch.Tensor

Alias for field number 0

v_leak: torch.Tensor

Alias for field number 3

v_reset: torch.Tensor

Alias for field number 5

v_th: torch.Tensor

Alias for field number 4

class norse.torch.functional.LSNNState(z: torch.Tensor, v: torch.Tensor, i: torch.Tensor, b: torch.Tensor)[source]

Bases: tuple

State of an LSNN neuron

Parameters

Create new instance of LSNNState(z, v, i, b)

b: torch.Tensor

Alias for field number 3

i: torch.Tensor

Alias for field number 2

v: torch.Tensor

Alias for field number 1

z: torch.Tensor

Alias for field number 0

class norse.torch.functional.STDPSensorParameters(eta_p: torch.Tensor = tensor(1.), eta_m: torch.Tensor = tensor(1.), tau_ac_inv: torch.Tensor = tensor(10.), tau_c_inv: torch.Tensor = tensor(10.))[source]

Bases: tuple

Parameters of an STDP sensor as it is used for event driven plasticity rules.

Parameters

Create new instance of STDPSensorParameters(eta_p, eta_m, tau_ac_inv, tau_c_inv)

eta_m: torch.Tensor

Alias for field number 1

eta_p: torch.Tensor

Alias for field number 0

tau_ac_inv: torch.Tensor

Alias for field number 2

tau_c_inv: torch.Tensor

Alias for field number 3

class norse.torch.functional.STDPSensorState(a_pre: torch.Tensor, a_post: torch.Tensor)[source]

Bases: tuple

State of an event driven STDP sensor.

Parameters

Create new instance of STDPSensorState(a_pre, a_post)

a_post: torch.Tensor

Alias for field number 1

a_pre: torch.Tensor

Alias for field number 0

norse.torch.functional.circ_dist_fn(x, k)[source]
norse.torch.functional.coba_lif_feed_forward_step(input_tensor, state, p=CobaLIFParameters(tau_syn_exc_inv=tensor(0.2000), tau_syn_inh_inv=tensor(0.2000), c_m_inv=tensor(5.), g_l=tensor(0.2500), e_rev_I=tensor(- 100), e_rev_E=tensor(60), v_rest=tensor(- 20), v_reset=tensor(- 70), v_thresh=tensor(- 10), method='super', alpha=100.0), dt=0.001)[source]

Euler integration step for a conductance based LIF neuron.

Parameters
Return type

Tuple[Tensor, CobaLIFFeedForwardState]

norse.torch.functional.coba_lif_step(input_tensor, state, input_weights, recurrent_weights, p=CobaLIFParameters(tau_syn_exc_inv=tensor(0.2000), tau_syn_inh_inv=tensor(0.2000), c_m_inv=tensor(5.), g_l=tensor(0.2500), e_rev_I=tensor(- 100), e_rev_E=tensor(60), v_rest=tensor(- 20), v_reset=tensor(- 70), v_thresh=tensor(- 10), method='super', alpha=100.0), dt=0.001)[source]

Euler integration step for a conductance based LIF neuron.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (CobaLIFState) – current state of the neuron

  • input_weights (torch.Tensor) – input weights (sign determines contribution to inhibitory / excitatory input)

  • recurrent_weights (torch.Tensor) – recurrent weights (sign determines contribution to inhibitory / excitatory input)

  • p (CobaLIFParameters) – parameters of the neuron

  • dt (float) – Integration time step

Return type

Tuple[Tensor, CobaLIFState]

norse.torch.functional.constant_current_lif_encode(input_current, seq_length, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Encodes input currents as fixed (constant) voltage currents, and simulates the spikes that occur during a number of timesteps/iterations (seq_length).

Example

>>> data = torch.as_tensor([2, 4, 8, 16])
>>> seq_length = 2 # Simulate two iterations
>>> constant_current_lif_encode(data, seq_length)
 # State in terms of membrane voltage
(tensor([[0.2000, 0.4000, 0.8000, 0.0000],
         [0.3800, 0.7600, 0.0000, 0.0000]]),
 # Spikes for each iteration
 tensor([[0., 0., 0., 1.],
         [0., 0., 1., 1.]]))
Parameters

  • input_current (torch.Tensor) – The input tensor, representing LIF current

  • seq_length (int) – The number of iterations to simulate

  • p (LIFParameters) – Initial neuron parameters.

  • dt (float) – Time delta between simulation steps

Return type

Tensor

Returns

A tensor with an extra dimension of size seq_length containing spikes (1) or no spikes (0).

norse.torch.functional.correlation_based_update(ts, linear_update, weights, correlation_state, learning_rate, ts_frequency)[source]
norse.torch.functional.correlation_sensor_step(z_pre, z_post, state, p=CorrelationSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.)), dt=0.001)[source]

Euler integration step of an idealized version of the correlation sensor as it is present on the BrainScaleS 2 chips.

Return type

CorrelationSensorState

norse.torch.functional.create_izhikevich_spiking_behavior(a, b, c, d, v_rest, u_rest, tau_inv=250)[source]

A function that allows for the creation of custom Izhikevich neurons models, as well as a visualization of their behavior on a 250 ms time window :type a: float :param a: time scale of the recovery variable u. Smaller values result in slower recovery in 1/ms :type a: float :type b: float :param b: sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential v. Greater values couple v and u more strongly resulting in possible subthreshold oscillations and low-threshold spiking dynamics :type b: float :type c: float :param c: after-spike reset value of the membrane potential in mV :type c: float :type d: float :param d: after-spike reset of the recovery variable u caused by slow high-threshold Na+ and K+ conductances in mV :type d: float :type v_rest: float :param v_rest: resting value of the v variable in mV :type v_rest: float :type u_rest: float :param u_rest: resting value of the u variable :type u_rest: float :type tau_inv: float :param tau_inv: inverse time constant in 1/ms :type tau_inv: float :param current: input current :type current: float :param time_print: size of the time window in ms :type time_print: float :param timestep_print: timestep of the simulation in ms :type timestep_print: float

Return type

IzhikevichSpikingBehavior

norse.torch.functional.euclidean_distance(x, y)[source]

Simple euclidean distance metric.

norse.torch.functional.gaussian_rbf(tensor, sigma=1)[source]

A gaussian radial basis kernel that calculates the radial basis given a distance value (distance between \(x\) and a data value \(x'\), or \(\|\mathbf{x} - \mathbf{x'}\|^2\) below).

\[K(\mathbf{x}, \mathbf{x'}) = \exp\left(- \frac{\|\mathbf{x} - \mathbf{x'}\|^2}{2\sigma^2}\right)\]
Parameters

  • tensor (torch.Tensor) – The tensor containing distance values to convert to radial bases

  • sigma (float) – The spread of the gaussian distribution. Defaults to 1.

norse.torch.functional.heavi_circ_fn(x, k)[source]
norse.torch.functional.heavi_erfc_fn(x, k)[source]
norse.torch.functional.heavi_tanh_fn(x, k)[source]
norse.torch.functional.izhikevich_recurrent_step(input_current, s, input_weights, recurrent_weights, p, dt=0.001)[source]
Return type

Tuple[Tensor, IzhikevichRecurrentState]

norse.torch.functional.izhikevich_step(input_current, s, p, dt=0.001)[source]
Return type

Tuple[Tensor, IzhikevichState]

norse.torch.functional.li_feed_forward_step(input_tensor, state, p=LIParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.)), dt=0.001)[source]
Return type

Tuple[Tensor, LIState]

norse.torch.functional.li_step(input_tensor, state, input_weights, p=LIParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.)), dt=0.001)[source]

Single euler integration step of a leaky-integrator. More specifically it implements a discretized version of the ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

and transition equations

\[i = i + w i_{\text{in}}\]
Parameters
Return type

Tuple[Tensor, LIState]

norse.torch.functional.lif_adex_current_encoder(input_current, voltage, adaptation, p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of an adaptive exponential LIF neuron-model adapted from http://www.scholarpedia.org/article/Adaptive_exponential_integrate-and-fire_model. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{a} &= 1/\tau_{\text{ada}} \left( a_{current} (V - v_{\text{leak}}) - a \right) \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + i_{\text{in}} \\ a &= a + a_{\text{spike}} z_{\text{rec}} \end{align*}\end{split}\]
Parameters

  • input (torch.Tensor) – the input current at the current time step

  • voltage (torch.Tensor) – current state of the LIFAdEx neuron

  • adaptation (torch.Tensor) – membrane adaptation parameter in nS

  • p (LIFAdExParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, Tensor, Tensor]

norse.torch.functional.lif_adex_feed_forward_step(input_tensor, state=LIFAdExFeedForwardState(v=0, i=0, a=0), p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of an adaptive exponential LIF neuron-model adapted from http://www.scholarpedia.org/article/Adaptive_exponential_integrate-and-fire_model. It takes as input the input current as generated by an arbitrary torch module or function. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{a} &= 1/\tau_{\text{ada}} \left( a_{current} (V - v_{\text{leak}}) - a \right) \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + i_{\text{in}} \\ a &= a + a_{\text{spike}} z_{\text{rec}} \end{align*}\end{split}\]

where \(i_{\text{in}}\) is meant to be the result of applying an arbitrary pytorch module (such as a convolution) to input spikes.

Parameters
Return type

Tuple[Tensor, LIFAdExFeedForwardState]

norse.torch.functional.lif_adex_step(input_tensor, state, input_weights, recurrent_weights, p=LIFAdExParameters(adaptation_current=tensor(4), adaptation_spike=tensor(0.0200), delta_T=tensor(0.5000), tau_ada_inv=tensor(2.), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of an adaptive exponential LIF neuron-model adapted from http://www.scholarpedia.org/article/Adaptive_exponential_integrate-and-fire_model. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{a} &= 1/\tau_{\text{ada}} \left( a_{current} (V - v_{\text{leak}}) - a \right) \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \\ a &= a + a_{\text{spike}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LIFAdExState) – current state of the LIF neuron

  • input_weights (torch.Tensor) – synaptic weights for incoming spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • p (LIFAdExParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFAdExState]

norse.torch.functional.lif_correlation_step(input_tensor, state, input_weights, recurrent_weights, p=LIFCorrelationParameters(lif_parameters=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), input_correlation_parameters=CorrelationSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.)), recurrent_correlation_parameters=CorrelationSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.))), dt=0.001)[source]
Return type

Tuple[Tensor, LIFCorrelationState]

norse.torch.functional.lif_current_encoder(input_current, voltage, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Computes a single euler-integration step of a leaky integrator. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]
Parameters

  • input (torch.Tensor) – the input current at the current time step

  • voltage (torch.Tensor) – current state of the LIF neuron

  • p (LIFParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, Tensor]

norse.torch.functional.lif_ex_current_encoder(input_current, voltage, p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of a leaky integrator adapted from https://neuronaldynamics.epfl.ch/online/Ch5.S2.html. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]
Parameters

  • input (torch.Tensor) – the input current at the current time step

  • voltage (torch.Tensor) – current state of the LIFEx neuron

  • p (LIFExParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, Tensor]

norse.torch.functional.lif_ex_feed_forward_step(input_tensor, state=LIFExFeedForwardState(v=0, i=0), p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of an exponential LIF neuron-model adapted from https://neuronaldynamics.epfl.ch/online/Ch5.S2.html. It takes as input the input current as generated by an arbitrary torch module or function. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + i_{\text{in}} \end{align*}\end{split}\]

where \(i_{\text{in}}\) is meant to be the result of applying an arbitrary pytorch module (such as a convolution) to input spikes.

Parameters
Return type

Tuple[Tensor, LIFExFeedForwardState]

norse.torch.functional.lif_ex_step(input_tensor, state, input_weights, recurrent_weights, p=LIFExParameters(delta_T=tensor(0.5000), tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=100.0), dt=0.001)[source]

Computes a single euler-integration step of an exponential LIF neuron-model adapted from https://neuronaldynamics.epfl.ch/online/Ch5.S2.html. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} \left(v_{\text{leak}} - v + i + \Delta_T exp\left({{v - v_{\text{th}}} \over {\Delta_T}}\right)\right) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LIFExState) – current state of the LIF neuron

  • input_weights (torch.Tensor) – synaptic weights for incoming spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • p (LIFExParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFExState]

norse.torch.functional.lif_feed_forward_step(input_tensor, state, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Computes a single euler-integration step for a lif neuron-model. It takes as input the input current as generated by an arbitrary torch module or function. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + i_{\text{in}} \end{align*}\end{split}\]

where \(i_{\text{in}}\) is meant to be the result of applying an arbitrary pytorch module (such as a convolution) to input spikes.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • state (LIFFeedForwardState) – current state of the LIF neuron

  • p (LIFParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFFeedForwardState]

norse.torch.functional.lif_mc_feed_forward_step(input_tensor, state, g_coupling, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Computes a single euler-integration feed forward step of a LIF multi-compartment neuron-model.

Parameters
Return type

Tuple[Tensor, LIFFeedForwardState]

norse.torch.functional.lif_mc_refrac_feed_forward_step(input_tensor, state, g_coupling, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), dt=0.001)[source]
Return type

Tuple[Tensor, LIFRefracFeedForwardState]

norse.torch.functional.lif_mc_refrac_step(input_tensor, state, input_weights, recurrent_weights, g_coupling, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), dt=0.001)[source]
Return type

Tuple[Tensor, LIFRefracState]

norse.torch.functional.lif_mc_step(input_tensor, state, input_weights, recurrent_weights, g_coupling, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Computes a single euler-integration step of a LIF multi-compartment neuron-model.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LIFState) – current state of the neuron

  • input_weights (torch.Tensor) – synaptic weights for incoming spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • g_coupling (torch.Tensor) – conductances between the neuron compartments

  • p (LIFParameters) – neuron parameters

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFState]

norse.torch.functional.lif_refrac_feed_forward_step(input_tensor, state, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), dt=0.001)[source]
Computes a single euler-integration step of a feed forward

LIF neuron-model with a refractory period.

Parameters
Return type

Tuple[Tensor, LIFRefracFeedForwardState]

norse.torch.functional.lif_refrac_step(input_tensor, state, input_weights, recurrent_weights, p=LIFRefracParameters(lif=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), rho_reset=tensor(5.)), dt=0.001)[source]
Computes a single euler-integration step of a recurrently connected

LIF neuron-model with a refractory period.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LIFRefracState) – state at the current time step

  • input_weights (torch.Tensor) – synaptic weights for incoming spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • p (LIFRefracParameters) – parameters of the lif neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFRefracState]

norse.torch.functional.lif_step(input_tensor, state, input_weights, recurrent_weights, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Computes a single euler-integration step of a LIF neuron-model. More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}})\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LIFState) – current state of the LIF neuron

  • input_weights (torch.Tensor) – synaptic weights for incoming spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • p (LIFParameters) – parameters of a leaky integrate and fire neuron

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LIFState]

norse.torch.functional.lift(activation, p=None)[source]

Creates a lifted version of the given activation function which applies the activation function in the temporal domain. The returned callable can be applied later as if it was a regular activation function, but the input is now assumed to be a tensor whose first dimension is time.

Parameters

  • activation (Callable[[torch.Tensor, Any, Any], Tuple[torch.Tensor, Any]]) – The activation function that takes an input tensor, an optional state, and an optional parameter object and returns a tuple of (spiking output, neuron state). The returned spiking output includes the time domain.

  • p (Any) – An optional parameter object to hand to the activation function.

Returns

A :class:`.Callable`_ that, when applied, evaluates the activation function N times, where N is the size of the outer (temporal) dimension. The application will provide a tensor of shape (time, …).

norse.torch.functional.logical_and(x, y)[source]

Computes a logical and provided x and y are bitvectors.

norse.torch.functional.logical_or(x, y)[source]

Computes a logical or provided x and y are bitvectors.

norse.torch.functional.logical_xor(x, y)[source]

Computes a logical xor provided x and y are bitvectors.

norse.torch.functional.logistic_fn(x, k)[source]
norse.torch.functional.lsnn_feed_forward_step(input_tensor, state, p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), dt=0.001)[source]

Euler integration step for LIF Neuron with threshold adaptation. More specifically it implements one integration step of the following ODE

\[\begin{split}\\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{b} &= -1/\tau_{b} b \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}} + b)\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + \text{input} \\ b &= b + \beta z \end{align*}\end{split}\]
Parameters
Return type

Tuple[Tensor, LSNNFeedForwardState]

norse.torch.functional.lsnn_step(input_tensor, state, input_weights, recurrent_weights, p=LSNNParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), tau_adapt_inv=tensor(0.0012), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), beta=tensor(1.8000), method='super', alpha=100.0), dt=0.001)[source]

Euler integration step for LIF Neuron with threshold adaptation More specifically it implements one integration step of the following ODE

\[\begin{split}\begin{align*} \dot{v} &= 1/\tau_{\text{mem}} (v_{\text{leak}} - v + i) \\ \dot{i} &= -1/\tau_{\text{syn}} i \\ \dot{b} &= -1/\tau_{b} b \end{align*}\end{split}\]

together with the jump condition

\[z = \Theta(v - v_{\text{th}} + b)\]

and transition equations

\[\begin{split}\begin{align*} v &= (1-z) v + z v_{\text{reset}} \\ i &= i + w_{\text{input}} z_{\text{in}} \\ i &= i + w_{\text{rec}} z_{\text{rec}} \\ b &= b + \beta z \end{align*}\end{split}\]

where \(z_{\text{rec}}\) and \(z_{\text{in}}\) are the recurrent and input spikes respectively.

Parameters

  • input_tensor (torch.Tensor) – the input spikes at the current time step

  • s (LSNNState) – current state of the lsnn unit

  • input_weights (torch.Tensor) – synaptic weights for input spikes

  • recurrent_weights (torch.Tensor) – synaptic weights for recurrent spikes

  • p (LSNNParameters) – parameters of the lsnn unit

  • dt (float) – Integration timestep to use

Return type

Tuple[Tensor, LSNNState]

norse.torch.functional.poisson_encode(input_values, seq_length, f_max=100, dt=0.001)[source]

Encodes a tensor of input values, which are assumed to be in the range [0,1] into a tensor of one dimension higher of binary values, which represent input spikes.

See for example https://www.cns.nyu.edu/~david/handouts/poisson.pdf.

Parameters

  • input_values (torch.Tensor) – Input data tensor with values assumed to be in the interval [0,1].

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • f_max (float) – Maximal frequency (in Hertz) which will be emitted.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

Return type

Tensor

Returns

A tensor with an extra dimension of size seq_length containing spikes (1) or no spikes (0).

norse.torch.functional.population_encode(input_values, out_features, scale=None, kernel=<function gaussian_rbf>, distance_function=<function euclidean_distance>)[source]

Encodes a set of input values into population codes, such that each singular input value is represented by a list of numbers (typically calculated by a radial basis kernel), whose length is equal to the out_features.

Population encoding can be visualised by imagining a number of neurons in a list, whose activity increases if a number gets close to its “receptive field”.

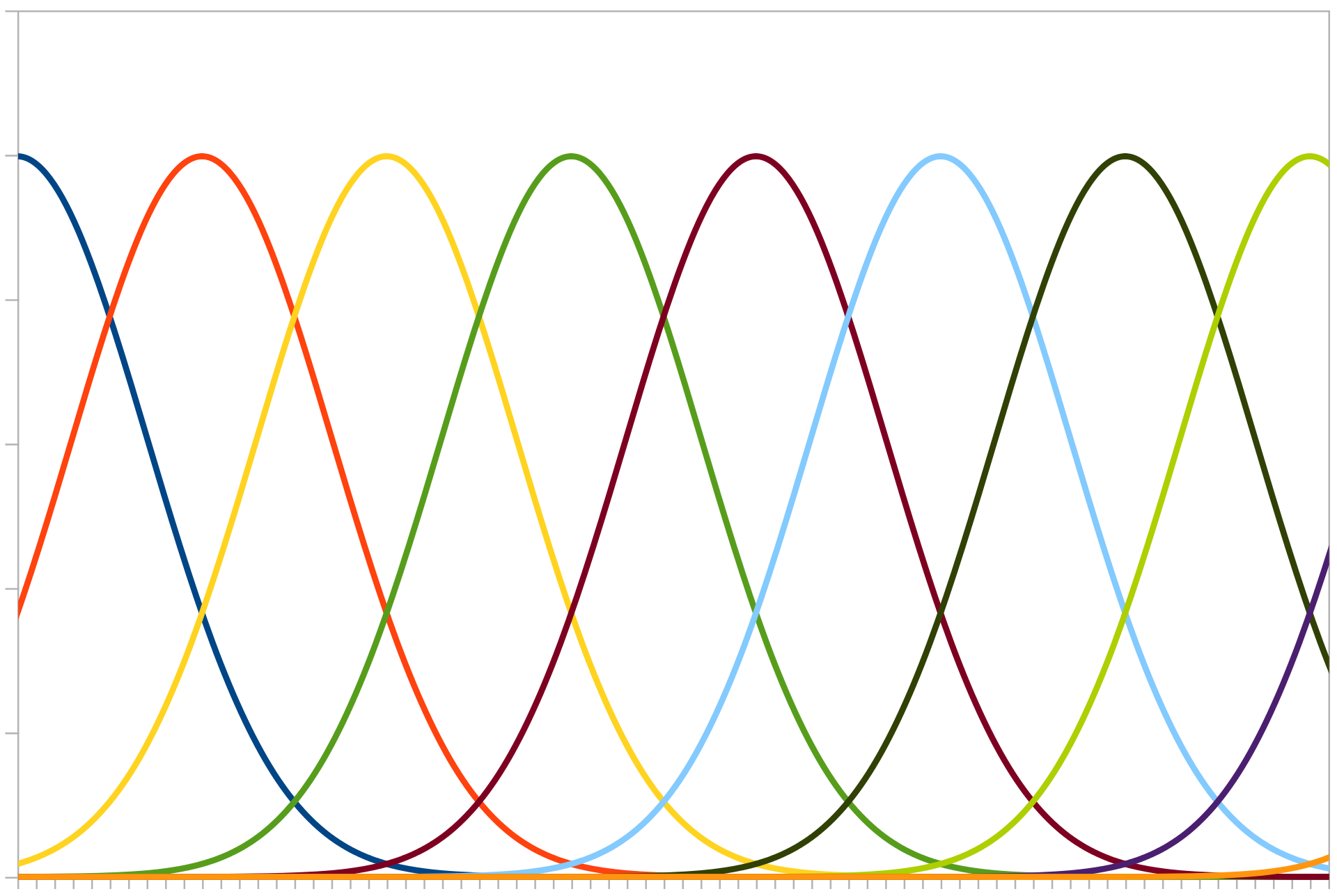
https://upload.wikimedia.org/wikipedia/commons/thumb/a/a1/PopulationCode.svg/1920px-PopulationCode.svg.png

Gaussian curves representing different neuron “receptive fields”. Image credit: Andrew K. Richardson.

Example

>>> data = torch.as_tensor([0, 0.5, 1])
>>> out_features = 3
>>> pop_encoded = population_encode(data, out_features)
tensor([[1.0000, 0.8825, 0.6065],
        [0.8825, 1.0000, 0.8825],
        [0.6065, 0.8825, 1.0000]])
>>> spikes = poisson_encode(pop_encoded, 1).squeeze() # Convert to spikes
Parameters

  • input_values (torch.Tensor) – The input data as numerical values to be encoded to population codes

  • out_features (int) – The number of output per input value

  • scale (torch.Tensor) – The scaling factor for the kernels. Defaults to the maximum value of the input. Can also be set for each individual sample.

  • kernel (Callable[[Tensor], Tensor]) – A function that takes two inputs and returns a tensor. The two inputs represent the center value (which changes for each index in the output tensor) and the actual data value to encode respectively.z Defaults to gaussian radial basis kernel function.

  • distance_function (Callable[[Tensor, Tensor], Tensor]) – A function that calculates the distance between two numbers. Defaults to euclidean.

Return type

Tensor

Returns

A tensor with an extra dimension of size seq_length containing population encoded values of the input stimulus. Note: An extra step is required to convert the values to spikes, see above.

norse.torch.functional.regularize_step(z, s, accumulator=<function spike_accumulator>, state=None)[source]

Takes one step for a regularizer that aggregates some information (based on the spike_accumulator function), which is pushed forward and returned for future inclusion in an error term.

Parameters

  • z (torch.Tensor) – Spikes from a cell

  • s (Any) – Neuron state

  • accumulator (Accumulator) – Accumulator that decides what should be accumulated

  • state (Optional[Any]) – The regularization state to be aggregated. Typically some numerical value like a count. Defaults to None

Return type

Tuple[Tensor, Any]

Returns

A tuple of (spikes, regularizer state)

norse.torch.functional.signed_poisson_encode(input_values, seq_length, f_max=100, dt=0.001)[source]

Encodes a tensor of input values, which are assumed to be in the range [-1,1] into a tensor of one dimension higher of binary values, which represent input spikes.

Parameters

  • input_values (torch.Tensor) – Input data tensor with values assumed to be in the interval [-1,1].

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • f_max (float) – Maximal frequency (in Hertz) which will be emitted.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

Return type

Tensor

Returns

A tensor with an extra dimension of size seq_length containing values in {-1,0,1}

norse.torch.functional.spike_accumulator(z, _, state=None)[source]

A spike accumulator that aggregates spikes and returns the total sum as an integer.

Parameters

  • z (torch.Tensor) – Spikes from some cell

  • s (Any) – Cell state

  • state (Optional[int]) – The regularization state to be aggregated to. Defaults to 0.

Return type

int

Returns

A new RegularizationState containing the aggregated data

norse.torch.functional.spike_latency_encode(input_spikes)[source]

For all neurons, remove all but the first spike. This encoding basically measures the time it takes for a neuron to spike first. Assuming that the inputs are constant, this makes sense in that strong inputs spikes fast.

See R. Van Rullen & S. J. Thorpe (2001): Rate Coding Versus Temporal Order Coding: What the Retinal Ganglion Cells Tell the Visual Cortex.

Spikes are identified by their unique position within each sequence.

Example

>>> data = torch.as_tensor([[0, 1, 1], [1, 1, 1]])
>>> spike_latency_encode(data)
tensor([[0, 1, 1],
        [1, 0, 0]])
Parameters

input_spikes (torch.Tensor) – A tensor of input spikes, assumed to be at least 2D (sequences, …)

Return type

Tensor

Returns

A tensor where the first spike (1) is retained in the sequence

norse.torch.functional.spike_latency_lif_encode(input_current, seq_length, p=LIFParameters(tau_syn_inv=tensor(200.), tau_mem_inv=tensor(100.), v_leak=tensor(0.), v_th=tensor(1.), v_reset=tensor(0.), method='super', alpha=tensor(100.)), dt=0.001)[source]

Encodes an input value by the time the first spike occurs. Similar to the ConstantCurrentLIFEncoder, but the LIF can be thought to have an infinite refractory period.

Parameters

  • input_current (torch.Tensor) – Input current to encode (needs to be positive).

  • sequence_length (int) – Number of time steps in the resulting spike train.

  • p (LIFParameters) – Parameters of the LIF neuron model.

  • dt (float) – Integration time step (should coincide with the integration time step used in the model)

Return type

Tensor

norse.torch.functional.stdp_sensor_step(z_pre, z_post, state, p=STDPSensorParameters(eta_p=tensor(1.), eta_m=tensor(1.), tau_ac_inv=tensor(10.), tau_c_inv=tensor(10.)), dt=0.001)[source]

Event driven STDP rule.

Parameters
Return type

STDPSensorState

norse.torch.functional.triangle_fn(x, alpha=0.3)[source]
Return type

Tensor

norse.torch.functional.voltage_accumulator(z, s, state=None)[source]

A spike accumulator that aggregates membrane potentials over time. Requires that the input state s has a v property (for voltage).

Parameters

  • z (torch.Tensor) – Spikes from some cell

  • s (Any) – Cell state

  • state (Optional[torch.Tensor]) – The regularization state to be aggregated to.

  • entries. (Defaults to zeros for all) –

Return type

int

Returns

A new RegularizationState containing the aggregated data

Subpackages