Working with Norse

3. Working with Norse#

For us, Norse is a tool to accelerate our own work within spiking neural networks (SNN). This page serves to describe the fundamental ideas behind the Python code in Norse and provide you with specific tools to become productive with SNN.

We will start by explaining some basic terminology, describe a suggestion to how Norse can be approached, and finally provide examples on how we have solved specific problems with Norse.

Table of content

  1. Terminology

  2. Norse workflow

  3. Solving deep learning problems with Norse

Note

You can execute the code below by hitting above and pressing Live Code.

3.1. Terminology#

3.1.1. Events and action potentials#

../_images/book-fig-spikes.png

Fig. 3.1 Illustration of discrete events, or spikes, from 10 neurons (y-axis) over 40 timesteps (x-axis) with events shown in white.#

Neurons are famous for their efficacy because they only react to sparse (rare) events called spikes or action potentials. In a spiking network less than \(2\%\) of the neurons are active at once. In Norse, therefore, we mainly operate on binary tensors of 0’s (no events) and 1’s (spike!). Fig. 3.1 illustrates such a random sampled data with exactly \(2\%\) activation.

3.1.2. Neurons and neuron state#

Neurons have parameters that determine their function. For example, they have a certain membrane voltage that will lead the neuron to spike if the voltage is above a threshold. Someone needs to keep track of that membrane voltage. If we wouldn’t, the neuron membrane would never update and we would never get any spikes. In Norse, we refer to that as the neuron state.

In code, it looks like this:

import torch
import norse.torch as norse

cell = norse.LIFCell()
data = torch.ones(1)
spikes, state = cell(data)        # First run is done without any state
# ...
spikes, state = cell(data, state) # Now we pass in the previous state
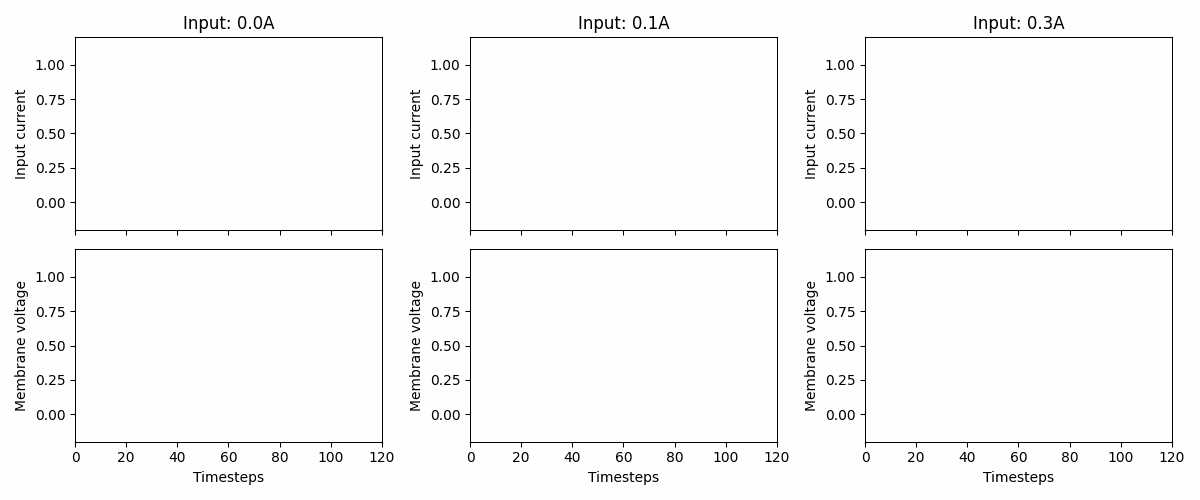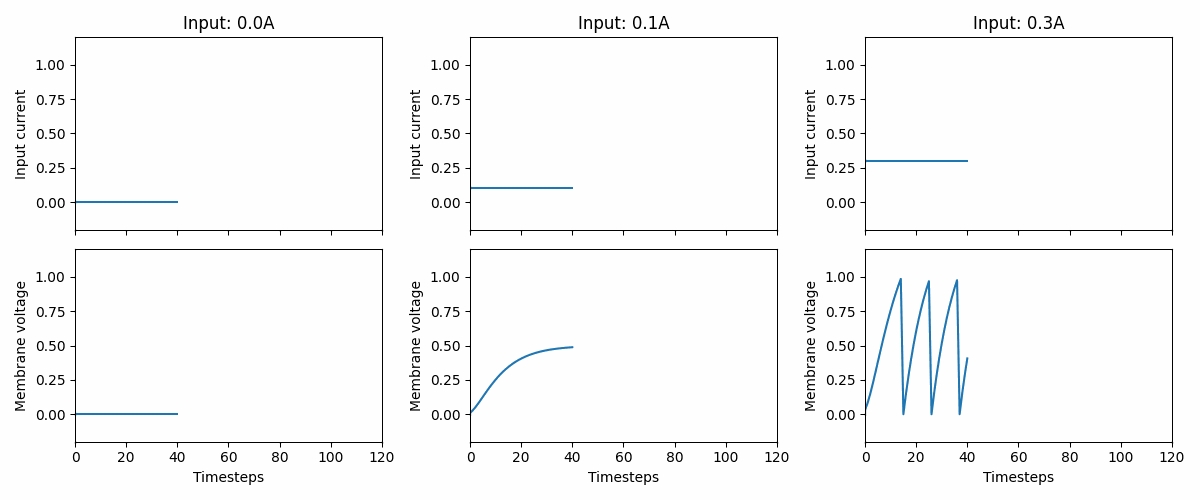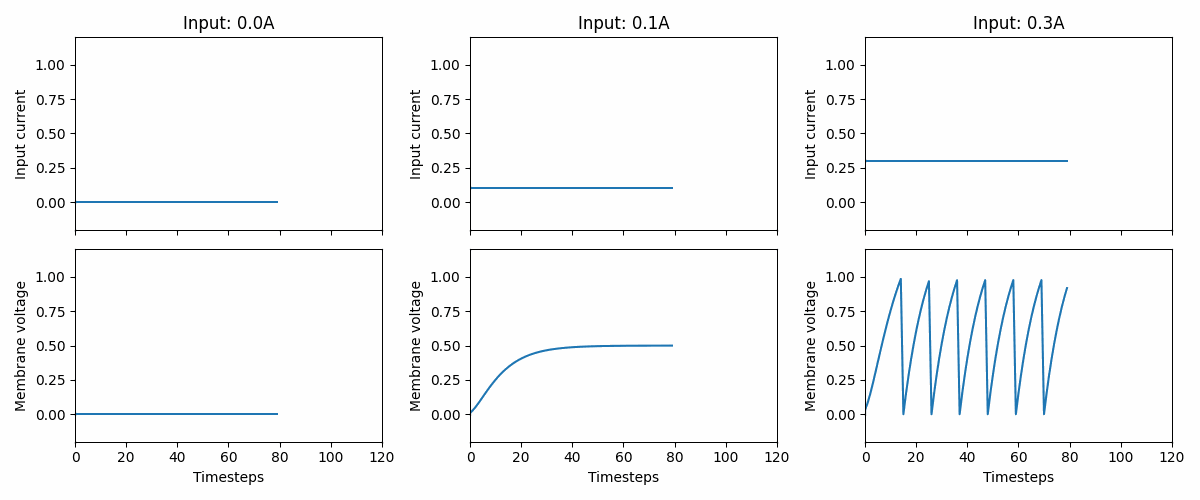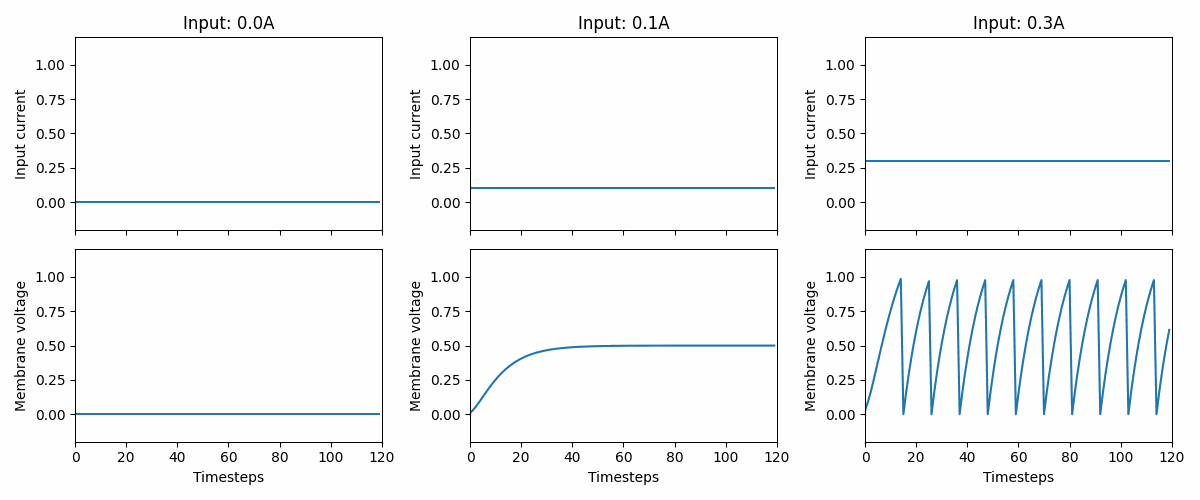
no-current

Fig. 3.2 Three examples of how the LIF neuron model responds to three different, but constant, input currents: 0.0, 0.1, and 0.3. At 0.3, we see that the neuron fires a series of spikes, followed by a membrane “reset”. Note that the neuron parameters are non-biological and that the memebrane voltage threshold is 1.#

States typically consist of two values: v (voltage), and i (current).

  • Voltage (v) illustrates the difference in “electric tension” in the neuron membrane. The higher the value, the more tension and better chance to arrive at a spike. In fig_working_ap the spike arrives at the peak of the curve, followed by an immediate reset and recovery. This is crucial for emitting spikes: if the voltage never increases - no spike!

  • Current (i) illustrates the incoming current, which will be integrated into the membrane potential v and decays over time.

3.1.3. Neuron dynamics and time#

Norse solves two of the hardest parts about running neuron simulations: neural equations and temporal dynamics. We provide a long list of neuron model implementations, as listed in our documentation that is free to plug’n’play.

For each model, we distinguish between time and recurrence as follows (using the Long short-term memory neuron model as an example):

Without time

With time

Without recurrence

LSNNCell

LSNN

With recurrence

LSNNRecurrentCell

LSNNRecurrent

In other words, the LSNNCell is not recurrent, and expects the input data to not have time, while the LSNNRecurrent is recurrent and expects the input to have time in the first dimension.

3.2. Norse workflow#

Norse is meant to be used as a library. Specifically, that means taking parts of it and remixing to fit the needs of a specific task. We have tried to provide useful, documented, and correct features from the spiking neural network domain, such that they become simple to work with.

The two main differences from artificial neural networks is 1) the state variables containing the neuron parameters and 2) the temporal dimension (see Introduction to spiking systems). Apart from that, Norse works like you would expect any PyTorch module to work.

When working with Norse we recommend that you consider two things

  1. Neuron models

  2. Learning algorithms and/or plasticity models

3.2.1. Deciding on neuron models#

The choice of neuron model depends on the task. Should the model be biologically plausible? Computationally efficient? … Two popular choices of models are the leaky integrate-and-fire neuron model, which will provide spiking output of either 0s or 1s. Another model is the leaky integrator, which will provide a voltage scalar output. Many more neuron models exist and can be found in our documentation: https://norse.github.io/norse/norse.torch.html#neuron-models

3.2.2. Deciding on learning/plasiticy models#

Optimization can be done using PyTorch’s gradient-based optimizations, as seen in the MNIST task. We have implemented SuperSpike and many other surrogate gradient methods that lets you seamlessly integrate with Norse. The surrogate gradient methods are documented here: https://norse.github.io/norse/norse.torch.functional.html#threshold-functions

If you require biological/local learning, we support plasticity via STDP and Tsodyks-Markram models.

3.3. Examples of deep learning problems in Norse#

Norse can be applied immediately for both fundamental research and deep learning problems.

To port existing deep learning problems, we can simply 1) replicate ANN architecture, 2) lift the signal in time (to allow the neurons time to react to the input signal), and 3) replace the ANN activation functions with SNN activation functions.

We have several examples of that in our tasks section, and MNIST is one of them; here we 1) build a convolutional network, 2) convert the MNIST dataset into sparse discrete events and 3) solve the task with LIF models, achieving >90% accuracy.

We can also replicate experiments from the literature, as shown in the memory task example. Here we use adaptive long short-term spiking neural networks to solve temporal memory problems.

Contents